Calculus - Week 2

Dive into the fundamentals of calculus for machine learning and data science. This week you’ll learn about partial derivatives, the gradient and multivariate optimization with gradient descent.

import re
from itertools import product

import matplotlib.pyplot as plt
import numpy as np
import plotly.graph_objects as go
import plotly.io as pio
import sympy as sp
from IPython.core.getipython import get_ipython
from IPython.display import display, HTML
from matplotlib.animation import FuncAnimation

plt.style.use("seaborn-v0_8-whitegrid")
pio.renderers.default = "plotly_mimetype+notebook"

Multivariate optimization

Tangent plane

The equation of the tangent line to \(f(x)\) at point \(x=a\) is

📐 \(y = \cfrac{d}{dx}f(a)(x-a) + f(a)\)

This is derived from the point-slope form of a line

\(y-y_1 = m(x-x_1)\)

The equation of the tangent plane to \(f(x, y)\) at point \(x=a\) and \(y=b\) is

📐 \(z = \cfrac{\partial}{\partial x}f(a)(x-a) + \cfrac{\partial}{\partial y}f(b)(y-b) + f(a, b)\)

which, similarly, is derived from the point-slope form of a plane

\(z-z_1 = m_1(x-x_1) + m_2(y-y_1)\)

def tangent_line(dfa, a, sym_a, a_range, b, sym_b, f):
    return (
        dfa.evalf(subs={sym_a: a, sym_b: b}) * (a_range - a)
        + f.evalf(subs={x: a, y: b})
    ).astype("float32")


def tangent_plane(dfa, dfb, a, a_range, b, b_range, f):
    return (
        dfa.evalf(subs={x: a, y: b}) * (a_range - a)
        + dfb.evalf(subs={x: a, y: b}) * (b_range - b)
        + f.evalf(subs={x: a, y: b})
    ).astype("float32")


x, y = sp.symbols("x, y")
parabloid = x**2 + y**2
dfx = sp.diff(parabloid, x)
dfy = sp.diff(parabloid, y)
x0 = 2
y0 = 4
full_range = np.linspace(-8, 8, 100)
y_cut_xx, y_cut_yy = np.meshgrid(full_range, np.linspace(-8, y0, 100))
xcut_xx, xcut_yy = np.meshgrid(np.linspace(-8, x0, 100), full_range)
full_xx, full_yy = np.meshgrid(full_range, full_range)
tan_x = np.linspace(x0 - 4, x0 + 4, 100)
tan_y = np.linspace(y0 - 4, y0 + 4, 100)
tan_xx, tan_yy = np.meshgrid(tan_x, tan_y)
const_x = np.full(100, x0)
const_y = np.full(100, y0)

ycut_parabloid_surface = go.Surface(
    z=sp.lambdify((x, y), parabloid, "numpy")(y_cut_xx, y_cut_yy),
    x=y_cut_xx,
    y=y_cut_yy,
    colorscale="Blues",
    contours=dict(x=dict(show=True), y=dict(show=True), z=dict(show=True)),
    colorbar=dict(orientation="h", y=-0.2, title=dict(text="z", side="top")),
    showlegend=True,
    legendgrouptitle_text="Partial derivative wrt x",
    legendgroup="x",
    name="y-cut parabloid",
)
xcut_parabloid_surface = go.Surface(
    z=sp.lambdify((x, y), parabloid, "numpy")(xcut_xx, xcut_yy),
    x=xcut_xx,
    y=xcut_yy,
    colorscale="Blues",
    contours=dict(x=dict(show=True), y=dict(show=True), z=dict(show=True)),
    colorbar=dict(orientation="h", y=-0.2, title=dict(text="z", side="top")),
    showlegend=True,
    legendgrouptitle_text="Partial derivative wrt y",
    legendgroup="y",
    name="x-cut parabloid",
)
full_parabloid_surface = go.Surface(
    z=sp.lambdify((x, y), parabloid, "numpy")(full_xx, full_yy),
    x=full_xx,
    y=full_yy,
    colorscale="Blues",
    contours=dict(x=dict(show=True), y=dict(show=True), z=dict(show=True)),
    colorbar=dict(orientation="h", y=-0.2, title=dict(text="z", side="top")),
    showlegend=True,
    name="full parabloid",
)
poi = go.Scatter3d(
    x=[x0],
    y=[y0],
    z=[sp.lambdify((x, y), parabloid, "numpy")(x0, y0)],
    marker=dict(color="#000000"),
    showlegend=True,
    name="x=2 y=4",
)
yparabola = go.Scatter3d(
    x=const_x,
    y=full_range,
    z=sp.lambdify((x, y), parabloid, "numpy")(const_x, full_range),
    mode="lines",
    line=dict(color="#000000", width=5),
    showlegend=True,
    legendgroup="y",
    name="y parabola",
)
ytangent = go.Scatter3d(
    x=const_x,
    y=tan_y,
    z=tangent_line(dfa=dfy, a=y0, sym_a=y, a_range=tan_y, b=x0, sym_b=x, f=parabloid),
    mode="lines",
    line=dict(color="#000000"),
    showlegend=True,
    legendgroup="y",
    name="y tangent",
)
xparabola = go.Scatter3d(
    x=full_range,
    y=const_y,
    z=sp.lambdify((x, y), parabloid, "numpy")(full_range, const_y),
    mode="lines",
    line=dict(color="#000000", width=5),
    showlegend=True,
    legendgroup="x",
    name="x parabola",
)
xtangent = go.Scatter3d(
    x=tan_x,
    y=const_y,
    z=tangent_line(dfa=dfx, a=x0, sym_a=x, a_range=tan_x, b=y0, sym_b=y, f=parabloid),
    mode="lines",
    line=dict(color="#000000"),
    showlegend=True,
    legendgroup="x",
    name="x tangent",
)
tangent_surface = go.Surface(
    z=tangent_plane(
        dfa=dfx, dfb=dfy, a=x0, a_range=tan_xx, b=y0, b_range=tan_yy, f=parabloid
    ),
    x=tan_xx,
    y=tan_yy,
    colorscale=[[0, "#FF8920"], [1, "#FF8920"]],
    showscale=False,
    name="tangent plane",
    showlegend=True,
)
fig = go.Figure(
    data=[
        full_parabloid_surface,
        xcut_parabloid_surface,
        ycut_parabloid_surface,
        poi,
        xtangent,
        xparabola,
        ytangent,
        yparabola,
        tangent_surface,
    ]
)
fig.update_layout(
    title="Tangent plane of parabloid at x=2 and y=4",
    autosize=False,
    width=600,
    height=600,
    margin=dict(l=10, r=10, b=10, t=30),
    legend=dict(groupclick="togglegroup", itemclick="toggleothers"),
    scene_camera=dict(
        eye=dict(x=1.5, y=1.5, z=0.5),
    ),
)
fig.show()

Partial derivatives

If we look at the tangent plane on the previous plot from a certain angle we’ll see two orthogonal lines, as if they were the axes of the plane.

😉 click on Reset camera to last save on the plot’s navbar to reset the eye to (x=1.5, y=1.5, z=.5)

The two lines that form the tangent plane are the tangent lines to the point and their respective slopes are called partial derivatives.

To visualize (or at least get a sense of it) the partial derivative:

\(\cfrac{\partial}{\partial x}f(x)\) at \(x=2\) select the legend group Partial derivative wrt x.

\(\cfrac{\partial}{\partial y}f(y)\) at \(y=4\) select the legend group Partial derivative wrt y.

In either case, we can see that the partial derivative is just the derivative of the imaginary 2D parabola that results from \(f(x, y)\) while keeping one of the two variables constant.

In fact, calculating partial derivatives is a 2-step process:

1. treat all the other variables as constants

2. apply the same rules of differentiations

For example, let \(f(x, y) = x^2+y^2\). To calculate \(\cfrac{\partial}{\partial x}x^2+y^2\) we

1. treat \(y\) as a constant, let’s say 1, but we don’t usually do this substitution in practice. We’ll do it here to drive the point home.

\(\cfrac{\partial f(x,y)}{\partial x} = x^2+1^2\)

2. apply the same rules of differentiations (in this case, power, constant and sum rules)

\(\cfrac{\partial f(x,y)}{\partial x} = 2x + 0\)

Let’s do another example. Let let \(f(x, y) = x^2y^2\).

We could do the same as before and replace \(y\) with 1, but in this case and more complex cases it might create more confusion than be helpful, as we’ll have to revert it back to \(y\) if it didn’t go away like it did in the previous example.

Let’s leave \(y\) as is and just treat as a constant. For the power and multiple constant rules we have

\(\cfrac{\partial f(x,y)}{\partial x} = 2xy^2\)

Equaling partial derivatives to 0 to find the minima and maxima

Let’s imagine we are in a sauna 5 meters wide and 5 meters long. We want to find the coldest place in the room.

Conveniently we know the function of the temperature in terms of the room coordinates.

x, y = sp.symbols("x, y")
temp = 50 - sp.Rational(1, 50) * x**2 * (x - 6) * y**2 * (y - 6)
temp

$\displaystyle - \frac{x^{2} y^{2} \left(x - 6\right) \left(y - 6\right)}{50} + 50$

room_size = 5
xx, yy = np.meshgrid(np.linspace(0, room_size, 100), np.linspace(0, room_size, 100))

surface = go.Surface(
    z=sp.lambdify((x, y), temp, "numpy")(xx, yy),
    x=xx,
    y=yy,
    colorscale="RdBu_r",
    contours=dict(x=dict(show=True), y=dict(show=True), z=dict(show=True)),
    colorbar=dict(title="Temperature"),
    name="temperature function",
)

fig = go.Figure(surface)
fig.update_layout(
    title="Function of the sauna temperature",
    autosize=False,
    width=600,
    height=600,
    scene_aspectmode="cube",
    margin=dict(l=10, r=10, b=10, t=30),
    scene_camera=dict(
        eye=dict(x=2.1, y=0.1, z=0.7),
    ),
)
fig.show()

Let’s calculate the partial derivative wrt x.

dfx = sp.diff(temp, x).factor()
dfx

$\displaystyle - \frac{3 x y^{2} \left(x - 4\right) \left(y - 6\right)}{50}$

Let’s calculate the partial derivative wrt y.

dfy = sp.diff(temp, y).factor()
dfy

$\displaystyle - \frac{3 x^{2} y \left(x - 6\right) \left(y - 4\right)}{50}$

Let’s check where the partial derivatives are 0.

solutions = {"x": set(), "y": set()}
for s in sp.solve(dfx) + sp.solve(dfy):
    for k, v in s.items():
        if v <= room_size:
            solutions[str(k)].add(float(v))
solutions = list(product(solutions["x"], solutions["y"]))

zs = []
for s in solutions:
    z = sp.lambdify((x, y), temp, "numpy")(s[0], s[1])
    zs.append(z)
    fig.add_scatter3d(
        x=[s[0]],
        y=[s[1]],
        z=[z],
        marker=dict(color="#67001F" if z > 40 else "#053061"),
        name="maximum" if z > 40 else "minimum",
    )
fig.update_layout(
    title="Maxima and minima of the function",
    showlegend=False,
    scene_camera=dict(
        eye=dict(x=2.0, y=-1.0, z=0.2),
    ),
)
fig.show()

Let’s show the tangent plane at the minimum point.

x0, y0 = solutions[np.argmin(zs)]
tan_x = np.linspace(x0 - 1, x0 + 1, 100)
tan_y = np.linspace(y0 - 1, y0 + 1, 100)
tan_xx, tan_yy = np.meshgrid(tan_x, tan_y)
const_x = np.full(100, x0)
const_y = np.full(100, y0)

ytangent = go.Scatter3d(
    x=const_x,
    y=tan_y,
    z=tangent_line(dfa=dfy, a=y0, sym_a=y, a_range=tan_y, b=x0, sym_b=x, f=temp),
    mode="lines",
    line=dict(color="#000000"),
    showlegend=True,
    legendgroup="y",
    name="y tangent",
)

xtangent = go.Scatter3d(
    x=tan_x,
    y=const_y,
    z=tangent_line(dfa=dfx, a=x0, sym_a=x, a_range=tan_x, b=y0, sym_b=y, f=temp),
    mode="lines",
    line=dict(color="#000000"),
    showlegend=True,
    legendgroup="x",
    name="x tangent",
)

tangent_surface = go.Surface(
    z=tangent_plane(
        dfa=dfx, dfb=dfy, a=x0, a_range=tan_xx, b=y0, b_range=tan_yy, f=temp
    ),
    x=tan_xx,
    y=tan_yy,
    colorscale=[[0, "#FF8920"], [1, "#FF8920"]],
    showscale=False,
    name="tangent plane",
    showlegend=True,
)

fig.add_traces([ytangent, xtangent, tangent_surface])
fig.update_layout(
    title="Tangent plane at the minimum",
)
fig.show()

Gradient

🔑 The gradient of \(f\) is a vector, each element of which is a partial derivative of \(f\)

\(\nabla f(x_1, x_2, \cdots, x_n) = \langle \cfrac{\partial f}{\partial x_1}, \cfrac{\partial f}{\partial x_2}, \cdots, \cfrac{\partial f}{\partial x_n} \rangle\)

Assume we are at \(\vec{p}\) in the domain space of \(f\) within \(\mathbb{R}^3\):

\(\vec{p} = \begin{bmatrix}0.3\\0.2\\0.8\\\end{bmatrix}\)

Upon calculating the partial derivatives of \(f(\vec{p})\), suppose we obtain the gradient:

\(\nabla f(\vec{p}) = \begin{bmatrix}0.05\\-0.2\\-0.1\end{bmatrix}\)

This implies that:

• The function \(f\) is increasing if we move to the right in the first dimension because the slope is positive

• The function \(f\) is increasing if we move to the left in the other two dimensions because the slope is negative

Furthermore, the second dimension has the steepest ascent, while the first dimension has the flattest.

🔑 \(\nabla f\) provides the direction and rate of fastest increase of \(f\), while \(-\nabla f\) provides the direction and rate of fastest decrease of \(f\)

nabla = sp.lambdify(
    (x, y), sp.Matrix([sp.diff(temp, x), sp.diff(temp, y)]), "numpy"
)
p0 = np.array([1.0, 3.0])
g0 = nabla(*p0)
xx, yy = np.meshgrid(np.linspace(0, 5, 100), np.linspace(0, 5, 100))
cs = plt.contourf(
    xx, yy, sp.lambdify((x, y), temp, "numpy")(xx, yy), levels=20, cmap="RdBu_r"
)
plt.scatter(p0[0], p0[1], color="k")
plt.quiver(
    p0[0],
    p0[1],
    -g0[0],
    -g0[1],
    angles="xy",
    scale_units="xy",
    scale=10,
    color="k",
)
plt.xlabel("x")
plt.ylabel("y")
plt.gca().set_aspect("equal")
plt.title(f"Negative gradient stemming from ${sp.latex(p0)}$")
plt.colorbar(cs, label="z")
plt.show()

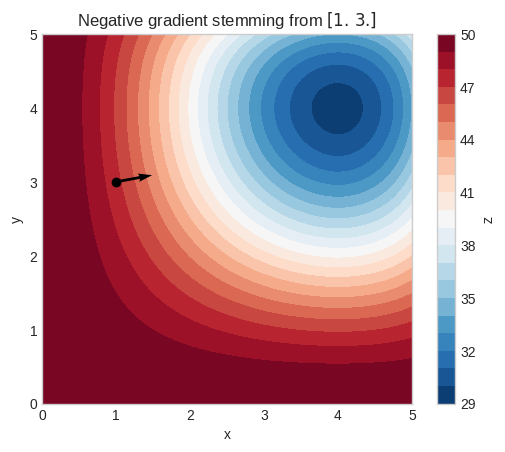
Continuing the previous example in \(\mathbb{R}^3\), if our goal is to find a minimum of the function \(f\), one approach is to update our position by taking a step of size \(S\) in the opposite direction of the gradient:

\(\vec{p}_{next} = \langle 0.3, 0.2, 0.8 \rangle - S \cdot \text{sign}(\langle 0.05, -0.2, -0.1 \rangle)\)

This approach doesn’t use all the information contained in the gradient, just the direction. It’s important to use also the steepness of the slope, so that we can take a larger step size if it’s very steep (far from the minimum) and a smaller step size if it’s flat (near the minimum.)

A better approach involves taking a step proportional to the value of the negative gradient.

\(\vec{p}_{next} = \langle 0.3, 0.2, 0.8 \rangle - \alpha \cdot \langle0.05, -0.2, -0.1 \rangle\)

🔑 \(\alpha\) is called learning rate and controls the step size

The above is the main idea of the gradient descent algorithm.

Below the pseudocode of a typical implementation of the gradient descent algorithm for \(T\) steps or until convergence, where convergence is define in terms of the norm of the gradient.

\(\begin{array}{l} \textbf{Algorithm: } \text{Gradient Descent} \\ \textbf{Input: } \text{initial parameters } p_0, \text{ learning rate } \alpha, \text{ number of iterations } T, \text{ convergence } \epsilon \\ \textbf{Output: } \text{final parameters } p\\ \phantom{0}1 : p \gets p_0 \\ \phantom{0}2 : \text{evaluate gradient } \nabla f(p) \\ \phantom{0}3 : \text{for i = 1 to T do} \\ \phantom{0}4 : \quad p_{new} \gets p - \alpha \nabla f(p) \\ \phantom{0}5 : \quad \text{evaluate gradient } \nabla f(p_{new}) \\ \phantom{0}6 : \quad \text{if } \|\nabla f(p_{new})\| < \epsilon \text{ then} \\ \phantom{0}7 : \quad \quad \text{return } p_{new} \\ \phantom{0}8 : \quad \text {end if} \\ \phantom{0}9 : \quad p \gets p_{new} \\ 10: \text{end for} \\ 11: \text{return } p \end{array}\)

🔑 Gradient descent is an iterative algorithm that uses the information contained in the gradient at a point to find the local minimum of a differentiable function

def bivariate_gradient_descent(f, symbols, initial, steps, learning_rate):
    x, y = symbols
    nabla = sp.lambdify(
        (x, y), sp.Matrix([sp.diff(f, x), sp.diff(f, y)]), "numpy"
    )
    p = np.zeros((steps, 2))
    g = np.zeros((steps, 2))
    step_vector = np.zeros((steps, 2))
    p[0] = initial
    g[0] = nabla(*p[0]).squeeze()
    step_vector[0] = learning_rate * g[0]
    for i in range(1, steps):
        p[i] = p[i - 1] - step_vector[i - 1]
        g[i] = nabla(*p[i]).squeeze()
        step_vector[i] = learning_rate * g[i]
        if np.linalg.norm(g[i]) < 1e-4:
            break
    return p[:i], g[:i], step_vector[:i]


def fixup_animation_js(html_animation):
    html_animation = html_animation.replace(
        '<div class="anim-controls">',
        '<div class="anim-controls" style="display:none">',
    )
    animation_id = re.findall(r"onclick=\"(.*)\.", html_animation)[0]
    img_id = re.findall(r"<img id=\"(.*)\"", html_animation)[0]
    html_animation += f"""
<script language="javascript">
setupAnimationIntersectionObserver('{animation_id}', '{img_id}');
</script>
"""
    return html_animation


def gradient_descent_animation(f, symbols, initial, steps, learning_rate, lim, cmap):
    def _update(frame):
        global scat, quiv
        scat = ax.scatter(p[:frame, 0], p[:frame, 1], color="k")
        quiv = ax.quiver(
            p[:frame, 0],
            p[:frame, 1],
            -g[:frame, 0],
            -g[:frame, 1],
            angles="xy",
            scale_units="xy",
            scale=10,
            color="k",
        )

    x, y = symbols
    p, g, _ = bivariate_gradient_descent(f, symbols, initial, steps, learning_rate)
    fig, ax = plt.subplots()
    xx, yy = np.meshgrid(np.linspace(0, lim, 100), np.linspace(0, lim, 100))
    cs = ax.contourf(
        xx,
        yy,
        sp.lambdify((x, y), f, "numpy")(xx, yy),
        levels=20,
        cmap=cmap,
    )
    scat = ax.scatter([], [])
    quiv = ax.quiver([], [], [1e-6], [1e-6])
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    ax.set_aspect("equal")
    plt.colorbar(cs, label="z")
    plt.title(
        rf"Gradient descent from ${sp.latex(p[0])}$ with $\alpha={learning_rate}$"
    )
    ani = FuncAnimation(fig=fig, func=_update, frames=steps)
    html_animation = ani.to_jshtml(default_mode="loop")
    if "runtime" not in get_ipython().config.IPKernelApp.connection_file:
        html_animation = fixup_animation_js(html_animation)
    display(HTML(html_animation))
    plt.close()


gradient_descent_animation(
    temp,
    (x, y),
    initial=np.array([1, 3]),
    steps=10,
    learning_rate=0.1,
    lim=5,
    cmap="RdBu_r",
)

Once Loop Reflect

One of the major drawbacks of gradient descent is its sensitivity to the learning rate.

gradient_descent_animation(
    temp,
    (x, y),
    initial=np.array([1, 3]),
    steps=20,
    learning_rate=0.3,
    lim=5,
    cmap="RdBu_r",
)

Once Loop Reflect

Convergence is not necessarily guaranteed and the learning rate must be chosen carefully.

Another drawback of gradient descent is that convergence doesn’t guarantee we’ve reached the global minimum.

Let’s consider a function with multiple minima.

x, y = sp.symbols("x, y")
multi = (
    -(
        10 / (3 + 3 * (x - 0.5) ** 2 + 3 * (y - 0.5) ** 2)
        + 2 / (1 + 2 * ((x - 3) ** 2) + 2 * (y - 1.5) ** 2)
        + 3 / (1 + 0.5 * ((x - 3.5) ** 2) + 0.5 * (y - 4) ** 2)
    )
    + 10
)

xx, yy = np.meshgrid(np.linspace(0, 5, 100), np.linspace(0, 5, 100))

surface = go.Surface(
    z=sp.lambdify((x, y), multi, "numpy")(xx, yy),
    x=xx,
    y=yy,
    colorscale="BrBg_r",
    contours=dict(x=dict(show=True), y=dict(show=True), z=dict(show=True)),
    colorbar=dict(title="z"),
    name="multi function",
)

fig = go.Figure(surface)
fig.update_layout(
    title="Function with multiple minima",
    autosize=False,
    width=600,
    height=600,
    scene_aspectmode="cube",
    margin=dict(l=10, r=10, b=10, t=30),
    scene_camera=dict(
        eye=dict(x=-1.2, y=1.8, z=1.25),
    ),
)
fig.show()

In this case the choice of the initial values is very important.

gradient_descent_animation(
    multi,
    (x, y),
    initial=np.array([1, 3]),
    steps=50,
    learning_rate=0.2,
    lim=5,
    cmap="BrBG_r",
)

Once Loop Reflect

Let’s start just 0.2 to right along the x-axis and we get to a better minima, and yet not the global minimum.

gradient_descent_animation(
    multi,
    (x, y),
    initial=np.array([1.2, 3]),
    steps=50,
    learning_rate=0.2,
    lim=5,
    cmap="BrBG_r",
)

Once Loop Reflect

If we start a bit more to the left and we get to the global minimum.

gradient_descent_animation(
    multi,
    (x, y),
    initial=np.array([0.6, 3]),
    steps=50,
    learning_rate=0.2,
    lim=5,
    cmap="BrBG_r",
)

Once Loop Reflect